F.BOUF

Datums
Ellipsoïdes, géoïdes, projections et coordonnées

Sommaire : Pour modéliser la forme de la Terre : ellipsoïdes et géoïdes
Pour obtenir des représentations planes : les projections
Pour se repérer : les systèmes de coordonnées
Pour savoir de quoi on parle : les datums

Pour modéliser la forme de la Terre : ellipsoïdes et géoïdes

En allant du plus simple au plus complexe, la Terre peut être représentée par :

Question:
Pourquoi la Terre n'est-elle pas sphérique ?
Réponse :
La Terre est soumise à deux actions permanentes : celle de sa propre gravité, qui lui donne une forme à peu près sphérique, et l'accélération centrifuge due à sa rotation, qui la déforme en ellipsoïde.
Question:
A quoi sont dus les creux et les bosses du géoïde ?
Réponse:
A l'hétérogénéité des roches constituant la Terre.
La forme, l'épaisseur et la densité de la croûte terrestre sont variables. Et en profondeur, la composition et la température des roches ne sont pas homogènes non plus. Tout ceci modifie l'intensité et la direction de la pesanteur, donc la forme du géoïde. L'hétérogénéité de la croûte terrestre provoque des variations de quelques décimètres à quelques mètres, sur des distances de quelques km à 1000 km. Les variations de densité profondes se traduisent par des variations qui peuvent aller jusqu'à plus de 100 m, sur des zones de plusieurs milliers de km.
Question:
Pourquoi tout le monde n'utilise pas le même ellipsoïde pour représenter la terre ?
Réponse:
Dans chaque pays, les services de géodésie ont calculé les paramètres de l'ellipsoïde de référence à partir de leur propres observations. Les résultats sont bien sûr différents. La précision des observations est variable, mais surtout chacun a adopté l'ellipsoïde qui, localement, colle le mieux avec la forme de la Terre.
Depuis l'avènement des mesures spatiales, la tendance est d'employer un ellipsoïde "global", valable pour la Terre entière. Mais cet ellipsoïde n'est qu'une approximation de la forme réelle de la Terre, et, encore une fois, il y a autant de manières de faire cette approximation que de services géodésiques.
Question:
Pourquoi prend-t-on comme référence le géoïde, une surface équipotentielle de pesanteur ?
Réponse:
Historiquement, la référence des altitudes a presque toujours été le niveau moyen des mers, qui est (à quelques mètres près) une surface équipotentielle. C'est pratique. Alors que si on prend les altitudes par rapport à un ellipsoïde on peut avoir, par exemple, les plages du sud-ouest de l'Australie à -40m tandis que celles de la côte nord sont à +70m. Cela fait un peu désordre.
D'autre part une surface équipotentielle a la propriété d'être partout horizontale, c'est à dire perpendiculaire à la verticale observée sur le terrain, celle qui sert de référence au géomètres et aux cartographes quand ils font des visées.
Enfin on peut bien connaître le géoïde, car on mesure la pesanteur avec une grande précision, par gravimétrie ponctuelle, par observation satellitaire du niveau de la mer, et en interprétant les perturbations des trajectoires des satellites.
Question:
Il y a-t-il un seul géoïde ?
Réponse:
En théorie oui, à l'altitude de référence près. Tous les géoïdes devraient donc être concentriques. Et il n'y a pas de raison pour ne pas adopter le même partout. En pratique ces géoïdes sont définis par des points plus moins denses et précis selon les techniques employées.
D'autre part, étant exprimé en altitude par rapport à un ellipsoïde de référence, un même géoïde sera défini par des valeurs numériques différentes selon qu'on se réfère à un ellipsoïde ou à un autre.

Pour obtenir des représentations planes : les projections

Pour représenter la surface de la Terre sur une carte plane, le principe de base est de projeter les objets à représenter sur un plan, ou sur une surface développable : cylindre ou cône. (une surface développable est une surface que l'on mettre à plat sans l'étirer).


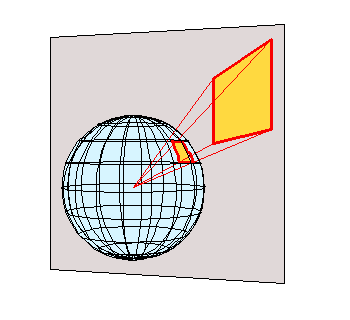
Projection sur un plan

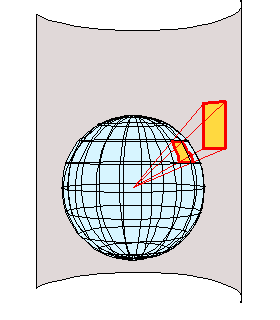
Projection sur un cylindre

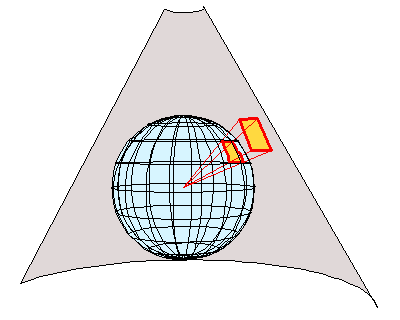
Projection sur un cône

Sur les schémas ci-dessus, chaque point est projeté suivant une ligne droite partant du centre du globe. En réalité, pour minimiser les distorsions, les projections employées sont plus complexes, et elles ne sont pas toujours représentables graphiquement.

Pour se repérer : les systèmes de coordonnées

Pour repérer un lieu, pour connaître la distance et le cap entre deux lieux, ont a besoin d'un système de coordonnées.

Les systèmes de coordonnées peuvent se classer en trois catégories selon qu'ils sont liés au globe terrestre, qu'ils résultent d'un système de projection, ou qu'il sont indépendants de l'un et de l'autre :

Les coordonnées liées au globe terrestre : latitude et longitude

La latitude d'un lieu est l'angle entre la verticale en ce lieu et le plan de l'équateur. La longitude est l'angle entre le plan méridien passant par la verticale et le plan méridien passant par la verticale d'un lieu de référence (ex : Greenwich). Ces définitions sont simples mais cela se complique quand on se demande ce qu'est la verticale. Est-ce le rayon terrestre qui passe par le lieu ? On utilise alors un modèle sphérique pour la terre. Est-ce la perpendiculaire à un ellipsoïde de référence ? On utilise un modèle ellipsoïdal (lequel, d'ailleurs). Est-ce la verticale observée ? On se base sur le géoïde.
Ces verticales sont -un peu- différentes, et un même lieu a donc des coordonnées géographiques (latitude et longitude) différentes selon la façon dont on approxime la forme de la Terre. Et les mêmes coordonnées correspondent à plusieurs lieux différents selon le système dans lequel elles sont exprimées. A l'échelle de la Terre la différence est minime, mais sur le terrain, plusieurs centaines de mètres, cela mérite d'être pris en considération.
D'autres différences plus triviales peuvent exister entre systèmes de coordonnées géographiques : le point de référence (Paris ou Greenwich, par exemple), l'unité d'angle employée (degrés ou grades).

Les coordonnées liées à un système de projection

A la base il s'agit du quadrillage régulier d'une carte construite selon un système de projection donné.
Par exemple :

Toutes les projections induisent des déformations.
Ces quadrillages ne représentent donc pas exactement des mètres sur le terrain, mais en sont très proches. Par exemple, une différence de 1000 en coordonnées UTM traduira une distance variant entre 999.60 et 1000.97 mètres selon le point où l'on est.
Plus important, les axes de coordonnées ne sont généralement pas orientés exactement nord-sud / est-ouest sur toute l'étendue de la projection. Par exemple, à Ouessant l'axe des Y des coordonnées "Lambert II étendu" est incliné de 5° 28' vers l'ouest, à Paris il est parfaitement sud-nord, et à Aléria il est incliné de 5° 16' vers l'est.

A noter que sur une carte peuvent figurer d'autres repères de coordonnées que celui qui est dérivé du système de projection utilisé. Ainsi sur les cartes au 1/25000 de l'IGN, en projection Lambert, on trouve les repères Lambert, UTM, géographiques international et français. Seul le quadrillage Lambert est parfaitement régulier, mais les autres repères sont néanmoins utilisables.

Les repères indépendants du globe et des projections : les repères cartésiens

Ce sont des repères orthonormés. Une origine : le centre de gravité de la Terre. Trois axes : l'axe des X dans le plan de l'équateur et dans le plan d'un méridien de référence, l'axe des Y lui aussi dans le plan de l'équateur et perpendiculaire à l'axe des X, l'axe des Z perpendiculaire au axes OX et OY et passant, à peu prés, par le pôle Nord.
Les avantages de ces repères sont qu'ils sont simples à définir et que les calculs y sont beaucoup plus faciles, donc plus rapides ou, à puissance égale, plus exacts. Leur gros inconvénient, c'est qu'ils sont à peu près inutilisables sur le terrain ou sur une carte. Ils sont donc cantonnés à des utilisations peu visibles de l'utilisateur : changement de repère, calcul de trajectoire de satellite, représentation 3D de la Terre ou d'autres corps célestes.
Les GPS, par exemple, affichent les coordonnées dans le système que vous voulez, les mémorisent en WGS84 (un système de coordonnées géographiques), mais font tous les calculs de positionnement en coordonnées cartésiennes.

Pour savoir de quoi on parle : les datums

De ce qui précède on déduit aisément que pour définir la position d'un lieu il ne suffit pas de donner ses coordonnées x et y, ni sa latitude et sa longitude, ni de dessiner un point sur une carte quelconque. Il faut aussi que soient précisés les modèles, les projections, les systèmes de coordonnée utilisés. Un datum (ou système géodésique) c'est un jeu cohérent de tout ces paramètres.

Il pourra comprendre :

En y ajoute parfois une date ou une triangulation de référence. La précision des levés et des calculs géodésiques s'accroît d'année en année. Il est utile de savoir à  partir de quels points, dont on connaît maintenant une position plus précise, ont été calculés les points cités. De plus, la dérive des continents n'est plus négligeable en regard de la précision atteinte.

Quelques exemples de Datums

WGS84 :

ED50 :

NTF :

-X------------------------ -------------------------X-